Fraction of the Sun's light absorbed by the Earth

June 2012

Introduction

We wish to calculate the fraction $f$ of the light emit from the sun that is absorbed by a planet. I will describe how to approximate the fraction of light absorbed by the planet in a couple of different ways. The planet is in an orbit of distance $a$ from the sun and that the planet has a radius of $b$. Measured in kilometers for the earth and sun, $a = 149000000$ and $b = 6378$.

Disc/sphere approximation

Let us first assume that the sun is a point source of light. The simplest approximation assumes that the radius of the planet is much smaller than the distance to the sun. This is a perfectly valid and reasonable assumption for celestial bodies. The area of a unit sphere is $4\pi$, and the solid angle of an object with respect to a point $p$ is equal to the area of the projection of the object onto a unit sphere centered at $p$. Because we assume that the sun emits light equally in all directions, the percentage of the light that falls on the planet will be the solid angle of the planet as seen from the sun.

When the solid angle of the planet is small ($b << a$), the projection of the planet onto a sphere will be nearly planar. If the projection is planar, the planet will form a disc with radius $\frac b a$. The area of this disk is $\pi \frac{b^2}{a^2}$. Dividing by the area of the unit sphere, we find that $$f = \frac{\pi \frac{b^2}{a^2}}{4\pi} = \frac{b^2}{4a^2}.$$

Point source approximation

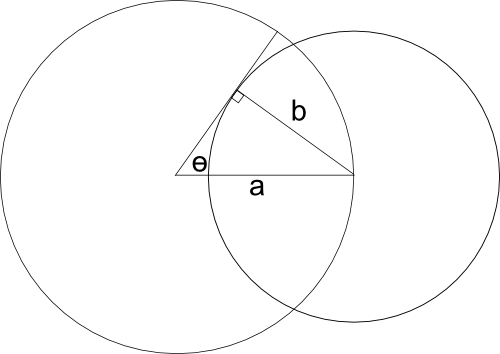
It is actually fairly easy to calculate the exact projection of the planet onto the unit sphere. If you fill the volume between the projected area and the sun, the shape will be a cone whose sides are tangent to the planet, and has an angle $\theta$ from the axis of symmetry. If we can find this angle, we can then calculate the solid angle of the planet's projection. A property of spheres is that any line that passes through a point on the sphere's surface and the sphere's center will be perpendicular to the plane tangent to the surface point. Thus, we have a right triangle shown in the figure, where two of the sides are known. We can therefore use the trigonometric identity that $$\sin(\theta)=\frac b a.$$

With $\theta$ known, we can use the formula that the solid angle is $$\Omega = 2\pi(1 - \cos(\theta)) = 2\pi(1 - \cos(\sin^{-1}(\frac b a))) = 2\pi\left(1 - \sqrt{1 - \frac{b^2}{a^2}}\right).$$ We can then find the fraction of light absorbed by the planet by dividing $\Omega$ by the area of the unit sphere, so $$f = \frac 1 2 \left(1 - \sqrt{1 - \frac{b^2}{a^2}}\right).$$