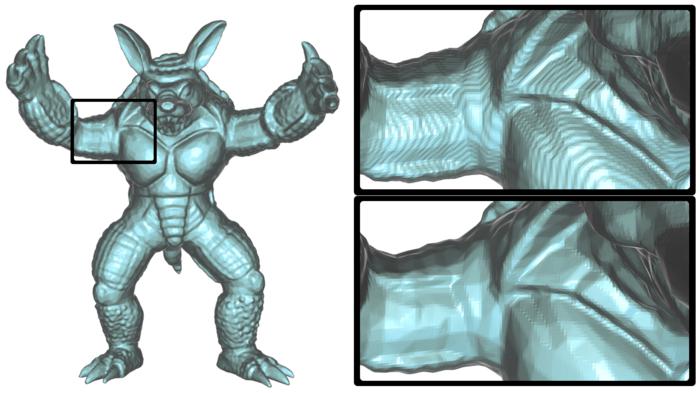
Contouring Discrete Indicator Functions

Discrete indicator functions are a special class of functions for which typical iso-surfacing methods produce poor results. We propose a new interpolant that does not generate the ridges that are generated by Marching Cubes on the same data.

download preprint

BibTeX

@article{Manson:2011:CDIF,
  author  = {Josiah Manson and
             Jason Smith and
             Scott Schaefer},
  title   = {Contouring Discrete Indicator Functions},
  journal = {Computer Graphics Forum (Proceedings of Eurographics)},
  year    = {2011},
  volume  = {30},
  number  = {2},
  pages   = {385--393},
}

Abstract

We present a method for calculating the boundary of objects from Discrete Indicator Functions that store 2-material volume fractions with a high degree of accuracy. Although Marching Cubes and its derivatives are effective methods for calculating contours of functions sampled over discrete grids, these methods perform poorly when contouring non-smooth functions such as Discrete Indicator Functions. In particular, Marching Cubes will generate surfaces that exhibit aliasing and oscillations around the exact surface. We derive a simple solution to remove these problems by using a new function to calculate the positions of vertices along cell edges that is efficient, easy to implement, and does not require any optimization or iteration. Finally, we provide empirical evidence that the error introduced by our contouring method is significantly less than is introduced by Marching Cubes.

Supplemental

contour_ours_fast.zip

3D contouring program that implements both our method and marching cubes.

contour_indicator_eg2011.pptx

Slides of presentation given by Jason Smith during Eurographics 2011.

License

The images, executables, and code supplied are from the web page http://josiahmanson.com. These materials are free to use for non-commercial purposes. Any works that use materials from this web page should acknowledge Josiah Manson and the paper Contouring Discrete Indicator Functions. For commercial use, please contact Josiah Manson (josiahmanson@gmail.com).